
某饲养场饲养宠物出售,设每头宠物每天至少需700g蛋白质,30g矿物质和100mg维生素。现有五种饲料可供选用
某饲养场饲养宠物出售,设每头宠物每天至少需700g蛋白质,30g矿物质和100mg维生素。现有五种饲料可供选用,各种饲料每kg营养成分含量及单价如下表所示。要求确定既满足... 某饲养场饲养宠物出售,设每头宠物每天至少需700g蛋白质,30g矿物质和100mg维生素。现有五种饲料可供选用,各种饲料每kg营养成分含量及单价如下表所示。要求确定既满足宠物生长的营养需要,又使费用最省的选用饲料的方案。(只建立线性规划模型,不必求解)
饲料 蛋白质(g) 矿物质(g) 维生素(mg) 价格(元/kg)
1 3 1 0.5 0.2
2 2 0.5 1 0.7
3 1 0.2 0.2 0.4
4 6 2 2 0.3
5 18 0.5 0.8 0.8 展开
解: 设总费用为Z。Xi(i=1,2,3,4,5)分别代表5种饲料。
目标函数:MinZ=0.2X1+0.7X2+0.4X3+0.3X4+0.8X5
约束条件:3X1+2X2+X3+6X4+18X5≥700
X1+0.5X2+0.2X3+2X4+0.5X5≥30
0.5X1+X2+0.2X3+2X4+0.8X5≥100
Xi(i=1,2,3,4,5)≥0
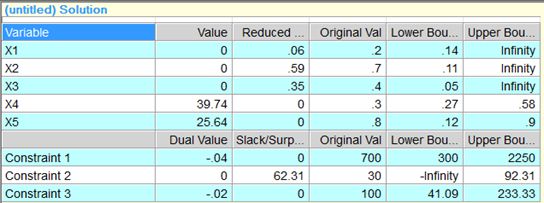
由模型解可知,使用4饲料39.74千克,5饲料25.64千克,最小费用为32.44元

评论(1)
举报 收起

北极雪wsy
2018-05-24 · TA获得超过16.1万个赞
知道大有可为答主

回答量:10.3万
采纳率:74%
帮助的人:8633万
关注
设1,2,3,4,5五种原料分别需要x,y,z,k,l;
最有=0.2x+0.7y+0.4z+0.3k+0.8l
{3x+2y+1z+6k+18l≤700;
x+0.5y+0.2z+2k+0.5l≤30;
0.5x+y+0.2z+2k+0.8l≤100
其中x,y,z,k,l≥0 }
你那数字编排的不太好……我是按
1,3 1 0.5 0.2
2,2 0.5 1 0.7
3,1 0.2 0.2 0.4
4,6 2 2 0.3
5,18 0.5 0.8 0.8
的排列列的计算式,若是数字对应错误,请自行修改

推荐律师服务: 若未解决您的问题,请您详细描述您的问题,通过百度律临进行免费专业咨询







